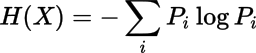「情報エントロピー」超入門｜ウィキペディアでは理解できなかったエンジニアのために…

エントロピーとはいっても高校化学で習った熱力学におけるエントロピーではありません。
機械学習（ランダムフォレストなど）の解説を見ているとでてくるアレです。

でも、エントロピーに関する説明をウィキペディアで読んだけどわからなかった、そんなことはありませんか？

それでは、ウィキペディアでの説明をみてみましょう。

情報理論においてエントロピーは確率変数が持つ情報の量を表す尺度で、それゆえ情報量とも呼ばれる。
確率変数Xに対し、XのエントロピーH(X)は

(ここでPiはX = iとなる確率)
で定義されており、これは統計力学におけるエントロピーと定数倍を除いて一致する。この定式化を行ったのはクロード・シャノンである。
これは単なる数式上の一致ではなく、統計力学的な現象に対して情報理論的な意味づけを与える事ができることを示唆する。
情報量は確率変数Xが数多くの値をとればとるほど大きくなる傾向があり、したがって情報量はXの取る値の「乱雑さ」を表す尺度であると再解釈できる。
よって情報量の概念は、原子や分子の「乱雑さの尺度」を表す統計力学のエントロピーと概念的にも一致する。

うーん、ちょっとピンときませんね。^^;
「確率変数が持つ情報の量を表す尺度」とか言われても理解できないですよ～

ただ、一行目に重要なことが書いてあります。

だそうです。

エントロピーは情報量とも呼ばれている、らしいです。

と考えてよいということですね。

エントロピーの計算式を考える前に、まず情報量とは一体何者なのかを考えてみましょう。

私達も「情報量」という言葉は日常的によく使います。
例えば、「このブログは情報量が多い」などと使います。
「情報量が多い」という言葉のニュアンスとしては、単に記事の文字が多いというより、記事内容が充実している、
といったことを指しているように思います。

例えば、次のような２つのブログ記事があったとします。

あなたは、どちらが情報量が多いと感じるでしょうか。
記事Aは１００文もありますが、得られる情報は「今日は雪だった」ということだけです。
一方、記事Bは少なくとも３つの情報が含まれています。「雪が降ったという事実」、「雪が降った原因」、「最低気温」といった情報が含まれています。

直感的には情報量は、記事B＞記事Aだといえるでしょう。

このような問題を感覚的ではなく、数学的に扱おうというのが情報理論（Information theory）という学問です。
エントロピー（情報エントロピー）は、情報理論の概念です。
情報理論の基本的な応用としては、ZIP、MP3などがあります。
とても身近な技術ということがお分かり頂けるかと思います。

さて、冒頭のウィキペディアの説明に戻りましょう。

さきほど直感的に情報量は、記事B＞記事Aであると書きました。
であれば、エントロピーも、記事B＞記事Aの関係が成り立つはずです。

それをこれから確認してみましょう。

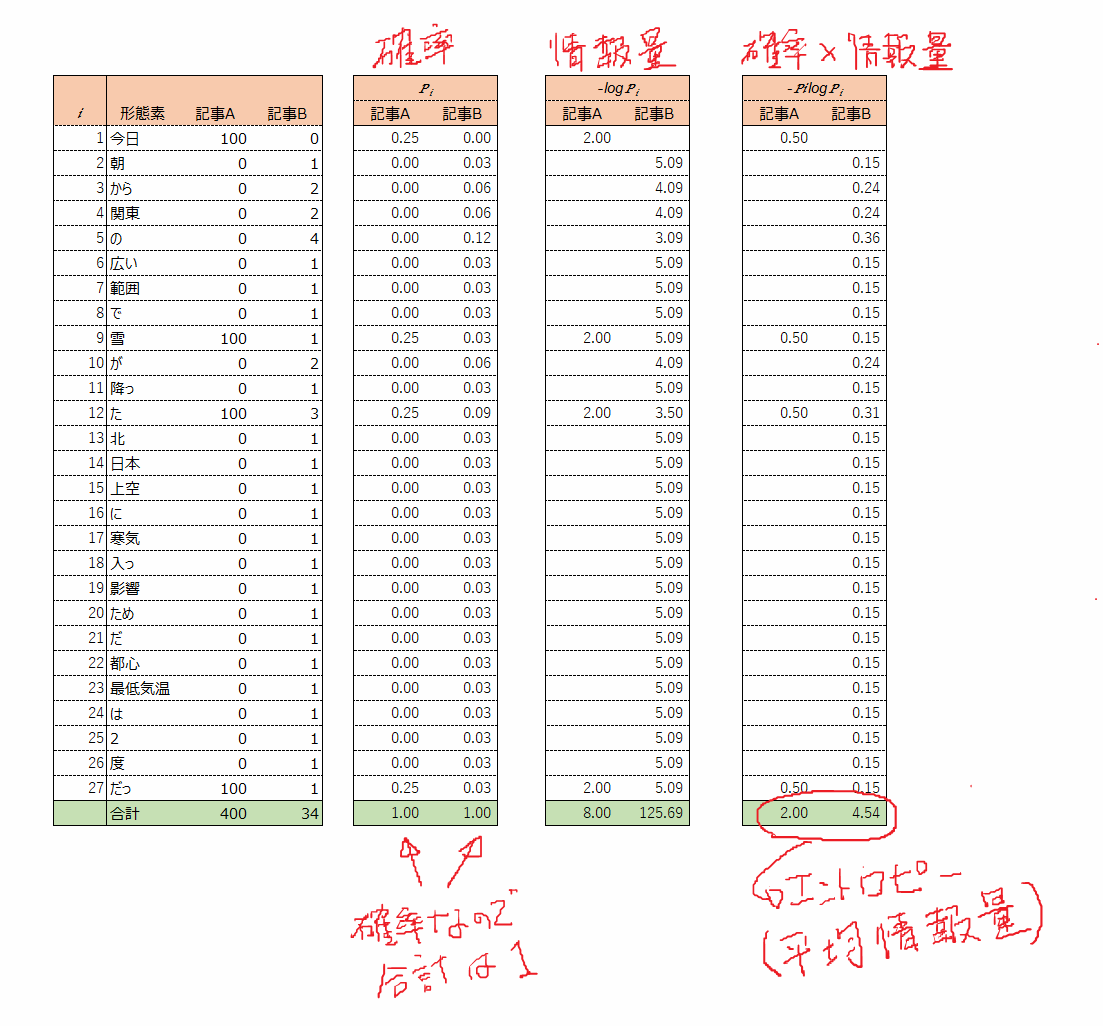
先程の記事A、Bを確率的に扱うために、形態素に分解してみます。
/(スラッシュ)は区切り位置がわかりやすいように記載しています。

続けて記事A、Bの形態素を数えて表にしてみます。
そして、先ほどのエントロピーの計算式に当てはめて、EXCELで計算しちゃいましょう。
結果は、記事Aが2.00、記事Bが5.45となり。
予想どおり、記事Bのほうがエントロピー（情報量）が高いという結果になりました。

計算式の解説については、また別日に追記したいと思います。

機械学習の概説が中心になりますが、基本的なことから勉強するなら以下の本がおすすめです。

■アマゾンで買うならこちら

■楽天で買うならこちら

事例＋演習で学ぶ機械学習 [ 速水悟 ] 価格：3024円（税込、送料無料) (2017/1/2時点)